

Project Momentum
Next Generation Knowledge Economy
Project Momentum
Next Generation Knowledge Economy
Chronicles of
BÖ§ZïK Inc.™ MSE/EPSE
Chronicles of
BÖ§ZïK Inc.™ MSE/EPSE


Project Momentum
Next Generation Knowledge Economy
Project Momentum
Next Generation Knowledge Economy
Chronicles of
BÖ§ZïK Inc.™ MSE/EPSE
Chronicles of
BÖ§ZïK Inc.™ MSE/EPSE
Newsflash! The Schedules for Physics II and
Pure Mathematics I & II are here!
COMPLEX NUMBER THEORY
Introduction
In this premier phase of the project, we will build on our previous study of the Real Number System, R. This leads to a most important extension, namely, the universal set and theory of Complex Numbers (Fig. 1). The Argand diagram, a revised 2-D system of representing numbers as vectors, will be used to visualize and analyze Complex Numbers.
Motivation
In the very early eras of solving algebraic equations, one of the many challenges encountered included the basic quadratic form:
Even with the use of robust techniques such as the quadratic formula, mathematicians and scientists encountered a daunting challenge of computing the square roots of its negative discriminant. At first, any conceivable solution seemed meaningless.
Definition and Innovation
As we will further discuss in our discovery sessions, the need to not discard the notion that a negative number has 2 positive square roots is valid. Hence, the definition of the “imaginary unit” of all complex numbers, i.
All scalar multiples of this unit forms an infinite set of imaginary numbers. For e.g., 2i, 7i and 2.6i. This give rise to the development of a complex number, which means any number that consists of a real and an imaginary part.
Complex Numbers have found its applications in very wide areas of applied mathematics (science and engineering, especially). It has become a formidable number system that is used to model elements of several real-time systems, such as power flow throughout the electric grid.
Giants in Mathematics and Science: Euler, Jacobi, Cauchy, Riemann, Descartes, Argand, de Moivre and many others: We thank you all!
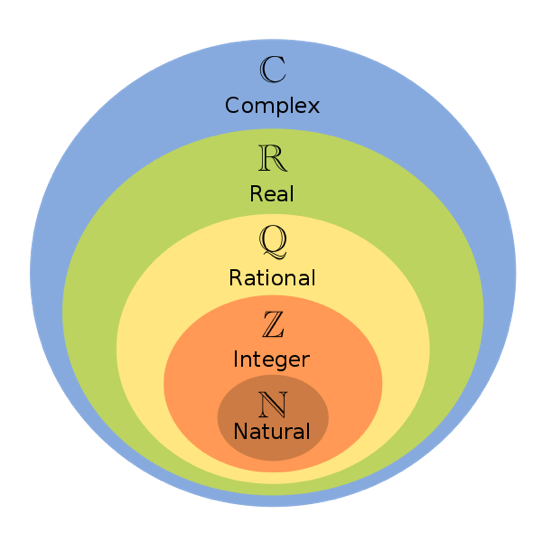
Fig. 1. The Number System, C
Modeling Complex Numbers as a Vector
So, in summary, a complex number is any number that is made up of a real and an imaginary part. The conventional symbol used for a complex number is z. And, the most commonly use “rectangular form” of a complex number is:
Here, the real and imaginary parts of the complex number are, respectively:
Using a modified cartesian plane calibrated and scaled with real numbers on its horizontal axis and imaginary numbers on its vertical axis, the rectangular form, z = a + bi, is developed (Fig. 2). Such a construct is called an Argand Diagram.
Notably, the length of a complex number is called the modulus (mod z) and the angle w.r.t. the positive real axis is called its argument (arg z).
The modulus and argument will be used to describe the polar form of z (shown in Fig. 3), which is directly equivalent to the rectangular form.

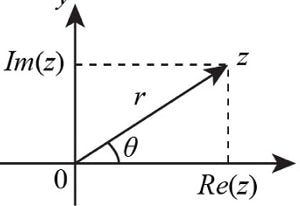
Fig. 2. The Argand Diagram
Fig. 3. A Polar vector
Innovation by G. David Boswell
under the auspices of BÖ§ZïK Inc.™ EPSE & MSE Syndicates
© 2022 & Beyond | All Publication Rights Reserved: Now and Beyond.