DECOMPOSITION TECHNOLOGY

Cloud Computing via Wolfram Alpha

Powered by the Mathematica computational engine, we leverage on the tremendous programming achievements by the engineers at the University of Illinois Urbana-Champaign, who we acknowledge for Wolfram Alpha. Included are selected Cloud Computing Widgets that you can use to experiment with algebraic operations of complex numbers.

Structure of Complex Numbers

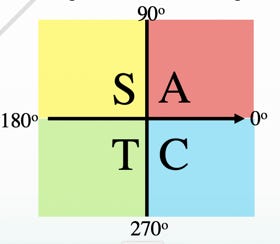
Any complex number, z, can be decomposed into a set of 4 dependent parts. This set is Re(z), Im(z), arg(z) and mod(z).

• • In the rectangular form, the real and imaginary parts are known such that: 
• • In the polar form, the modulus and the argument parts are known such that:   

• • The sine and cosine functions are used to decompose the polar to the rectangular form using:

• • Pythagoras’ Theorem and the arctangent definition are used to convert the rectangular to polar form using:

When finding the principal argument of a complex number, the “CAST logic” studied in trigonometry should be used.

Complex Numbers  Cloud Widgets

Calculations:  The Principal Argument

Great care must be exercised when computing the principal argument of a complex number from its rectangular form, z = a+bi. We should employ the CAST concept as a guide after correctly identifying the host Quadrant of z.

Consequently, there are 4 unique cases of calculating the argument (angle) of a complex number, z. With z located in any of the 4 quadrants, if α is the positive acute angle it makes with the real axis and θ = arg(z), then, in radians:

So, in the final analysis, the acceptable domain of the argument of z is: